Canon Science Lab
Light and Color
What would the world be like if there were no color? We can distinguish colors because our eyes detect Light. Let's take a look at how we perceive color.
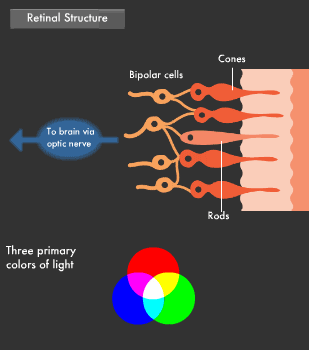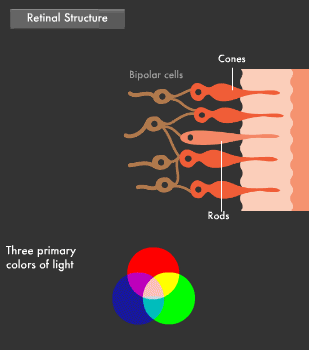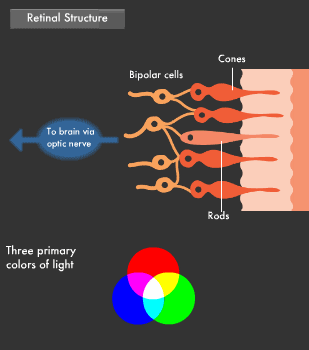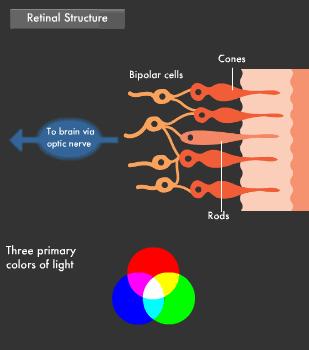
The human eye resembles a camera. It has an iris and a lens, and the retina-a membrane deep inside the eye-functions much like film. Light passes through the lens of the eye and strikes the retina, thereby stimulating its photoreceptor cells, which in turn emit a signal. This signal travels over the optic nerve to the brain, where color is perceived. There are two types of photoreceptor cells known as "cones" and "rods." Rods detect brightness and darkness, while cones detect color. Between the two, there are some 200 million photoreceptor cells. Cones are further classified into L, M, and S cones, each of which senses a different color wavelength, allowing us to perceive color.
Why Can We See Color?
Sunlight itself is colorless and is therefore called white light. So, why can we see color in the objects around us? An object's color depends on its properties. For example, an object that looks red when light is shined on it will appear bright red when only red light is used. When only blue light is used, however, the same object will look dark. An object that normally looks red reflects red light most intensely while absorbing other colors of light. In short, we see an object's color based on what color it is reflecting most intensely.
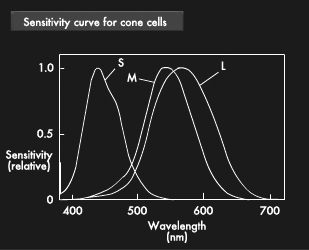
Light is comprised of the three primary colors: red, green and blue. Combining these three primary colors of light yields white, while other combinations can produce all the colors we see. The human retina has L, M and S cones, which act as sensors for red, green and blue, respectively.
Why do things appear in 3-D? (1)
The world as seen by humans is a 3-dimensional space. Why are we able to perceive the depth of objects despite the human retina sensing flat 2-dimensional information?
Humans have two eyes, which are separated horizontally (by a distance of approximately 6.5 cm). Because of this, the left eye and right eye view objects from slightly different angles (this is called "binocular disparity") and the images sensed by the retinas differ slightly. This difference is processed in the brain (in the visual area of the cerebral cortex) and recognized as 3-dimensional information.

Movie and television images are flat, 2-dimensional in nature, but 3-D movies and 3-D television utilize this "binocular disparity" to create different images for the left and right eyes. These two types of images are delivered to the left and right eyes, which provides the sensation of a 3-D image.
3-D movies generally require 3-D glasses to enable viewers to see two types of images on a single screen. Projection methods vary from theater to theater, as do the types of glasses used. Some typical types of 3-D glasses include color filter (anaglyph) glasses, polarized glasses, and shutter glasses. In the color filter method, images are divided into separate RGB wavelengths. When passed through glasses with different colored filters on the left and right lenses, the image matching each eye enters. In the polarization method, two types of polarized light differing by 90 degrees are applied to images, and these are separated using a polarization filter in the glasses. The shutter method switches between the left and right images. Shutter glasses alternate the opening and closing of the left and right shutters in sync with the switching of images on the screen, delivering the respective images to each eye. Because switching takes place over extremely short periods of time, the images appear without breaks due to the "afterimage effect" that takes place in human eyes.
Why do things appear in 3-D? (2)
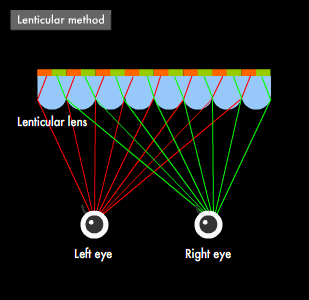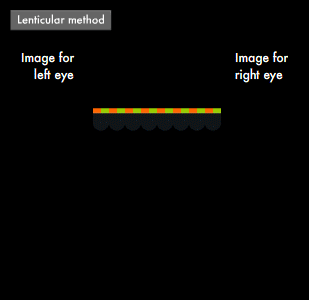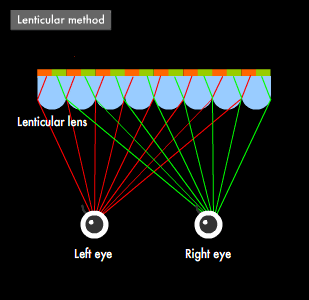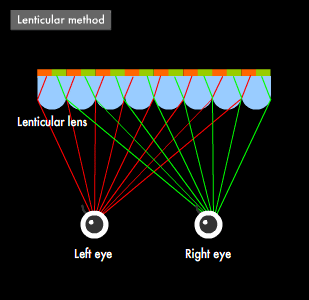
Like 3-D movies, 3-D televisions make use of "binocular disparity." The mechanism, however, is slightly different. 3-D televisions display two types of images by attaching optical components to the display panel or embedding fine slits in it. A typical optical component is the "lenticular lens," a lens sheet with a cross-section characterized by a semi-circular pattern, which is placed in front of the television screen, resulting in the image created by the pixels for each eye entering the left and right eyes of the viewer separately. This method enables viewers to enjoy 3-dimensional video without the need for special glasses, but the viewing location is limited. For example, when c represents the distance from the television screen to the lenticular lens, L the distance from the lenticular lens to the viewer, and f the focal length of the lenticular lens, the following relationship applies: 1/c + 1/L = 1/f. Once c and f have been determined, then the viewing position L becomes fixed. Furthermore, the frame sequential method, which alternates between two types of images without the use of optical components like the shutter method used in films, has recently been practically implemented for 3-D television and is becoming the most widely adopted technology. This method, however, requires glasses with shutters synchronized with the switching of images.
Other technologies that enable the world of 3-D to be enjoyed with even higher levels of realism are also being developed. A human's depth perception not only utilizes binocular disparity, but also "motion parallax," which enables not only the front of an object to be seen, but also the sides and back of the object when the object moves or is seen from a different angle. There are also systems that incorporate compact cameras and positional sensors like the HMD (head mounted display) used in Canon's MR (Mixed Reality) technology, which changes images in real time according to the movement of the viewer to provide a realistic 3-D video experience. Technology that makes use of holography is also under consideration.

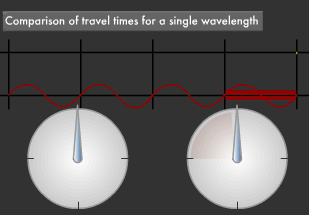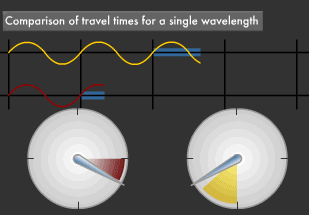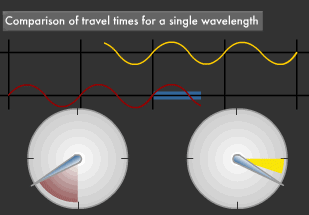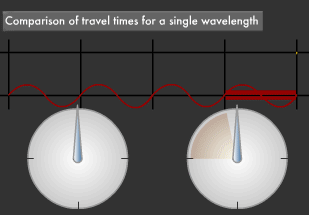
Does Light from Receding Objects Appear Reddish?
The "Doppler effect" acts on sound. For example, the pitch of an ambulance siren becomes higher as it moves toward you and lower as it moves away. This phenomenon occurs because many sound waves are squeezed into a shortening distance as the siren moves towards you, and stretched as the distance grows when the ambulance moves away from you. Light and sound are both waves, so the same phenomenon occurs with light, as well. Since the speed of light is extremely fast, this phenomenon can only be observed in space.
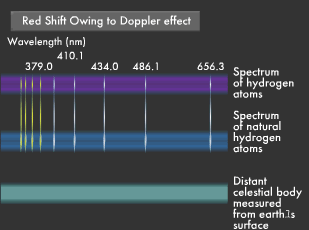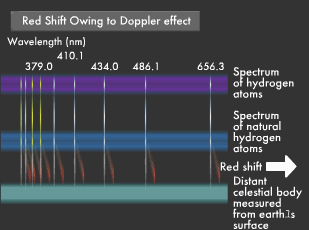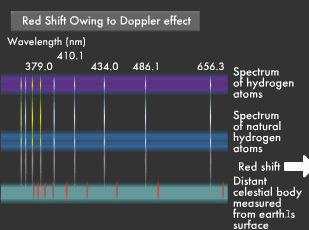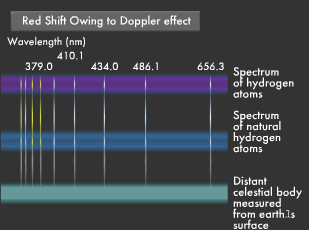
Light from stars approaching the earth has a shorter wavelength, appearing bluer than its true color, while light from stars receding into the distance has a longer wavelength, appearing reddish. These phenomena are known as blue shift and red shift, both of which are products of the Doppler effect.
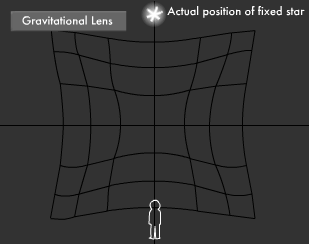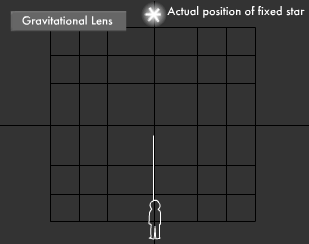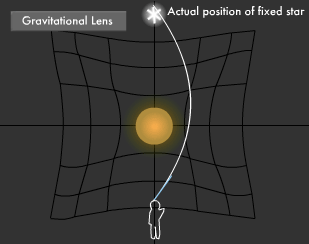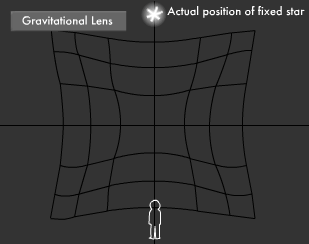
What Is the Gravitational Lens Effect?
Light behaves strangely in space. The gravitation lens effect produces this strange behavior. According to Einstein's General Theory of Relativity, an object that has mass (or weight, so to speak) will cause space-time to bend around it. Objects with extremely high mass will cause the surrounding space-time to bend even more. When such an object exists in outer space, light passing near it will travel along the curve it creates in space. By nature, light travels in a straight line, but when it encounters such an object in space-time, it bends much like it does when passing through a convex lens, hence the term gravitational lens effect.

When the light from a distant star is bent according to the gravitational lens effect, observers see the star as though it were in a different position than it really is. Just like a convex lens made of glass, this gigantic lens in space also forms images by enlarging stars and increasing brightness. Research on wobble in space and small stars that are dim and distant is underway at a fever pitch using this effect. Incidentally, when light from distant stars reaches the earth after skimming around the edge of the sun, gravitational refraction produces a lens-like effect that bends the light by an angle of 1.75 seconds (1 second is 1/3,600 degrees).
Does Gravity Change the Color of Light?
According to Einstein's General Theory of Relativity, an object that has mass will cause space-time to bend around it. Gravity is this very bending. We know that extremely large masses bend surrounding space-time tremendously and slowdown time. For example, a hypothetical clock on the sun's surface would tick slower than one on earth. When time slows in this manner, the wavelength of light from high-mass stars apparently gets longer by just the amount of slowdown. In short, the light will appear redder than it really is. This is called gravitational red shift.
Black holes, which are like "depressions" in outer space, have incredibly strong gravities, to the extent that even light itself will be drawn into them. We know that light attempting to escape from a black hole will be strongly red shifted due to the enormous gravity.

